3.1 Modèles en Variables d'Etat
3.1.3 Approximation des retards fractionnaires
Nouvelle formulation
Il apparaît que la classe d'approximation des retards fractionnaires,
du type filtre interpolateur de Lagrange (LIF), vérifie la
propriété dite de platitude maximale,
En conséquence la troncature à l'ordre N du développement en série entière de
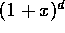avec x = 1/z - 1 correspond
exactement à la fonction de transfert du LIF d'ordre N.
Exprimé selon le schéma de Horner, cette fonction de transfert correspond
au diagramme-bloc suivant:
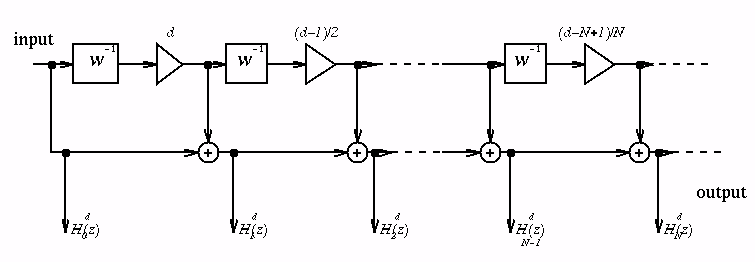
Avantages de la nouvelle structure
- Modularité,
- Diminution du coût de calcul,
- Sortie simultanée des filtres à tous les ordres,
- Changement d'ordre dynamique,
- Niveau de bruit acceptable pour des ordres raisonnables.
| Page remise à jour le Jeudi 14 novembre 1996 |
|
